這是史丹佛大學機器學習課程 Lecture 2 的錄影,而英文的 Lecture notes 可以從他的官方網站下載。
監督式學習(Supervised Learning)
以 Portland, Oregon 房屋資料為例,我們有房屋大小(living area)與房價(price)的資料:| 房屋大小(平方英尺) | 房價(千美元) |
| 2104 | 400 |
| 1600 | 330 |
| 2400 | 369 |
| 1416 | 232 |
| 3000 | 540 |
| ... | ... |
畫出來的 scatter plot 長成這樣:
那我們的問題是我們如何使用這些資料來預測其他在 Portland 的房價?更精確地說,就是如何使用方屋的大小推估房價?
為了能就方便建立嚴謹的數學模型,我們必須先定義一些接下來要常常使用的符號,以下是一些符號說明:
- \(x^{(i)}\):表示輸入的資料(input variable),也稱為輸入特徵(input features),在這個例子中就是房屋大小。
- \(y^{(i)}\):表示輸出的資料(output variable),也稱為目標變數(target variable),也就是我們想要估計的東西,在這裡就是指房價。
- \((x^{(i)}, y^{(i)})\):將一個 \(x^{(i)}\) 與 \(y^{(i)}\) 配對之後,稱為一組 training example。
- \(\{(x^{(i)}, y^{(i)}):i=1,...,m\}\):所有的 training examples 合起來稱為 training set,也就是指整個用來學習的資料庫。
- \(\mathcal{X}\):代表輸入資料的空間(space)。
- \(\mathcal{Y}\):代表輸出資料的空間,在這個例子中,\(\mathcal{X}\) 與 \(\mathcal{Y}\) 都是 \(\mathbb{R}\)。
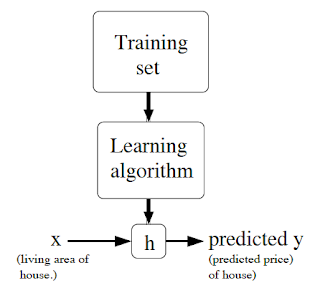
在這裡我們就是要找到一個從 \(\mathcal{X}\) 映射到 \(\mathcal{Y}\) 的函數 \(h(x)\),而這個函數可以靠著 \(x\) 來預測 \(y\),傳統上這個 \(h\) 就稱為一個 hypothesis,而整個流程就像這個圖:
當目標變數(target variable,也就是 \(y\))是連續型(continuous)的變數時,這樣的學習問題就稱為一個回歸(regression)問題,而當目標變數是離散型(discrete)的變數時(例如我們想預測該房屋是獨棟的還是公寓式的),那這個問題就稱為一個分類(classification)問題。
線性回歸(Linear Regression)
接著我們把剛剛的資料再加入一個輸入變數:每間房子的臥室數量:| 房屋大小(平方英尺) | 臥室數量 | 房價(千美元) |
| 2104 | 3 | 400 |
| 1600 | 3 | 330 |
| 2400 | 3 | 369 |
| 1416 | 2 | 232 |
| 3000 | 4 | 540 |
| ... | ... | ... |
一般來說在設計一個學習問題時,你可以自己決定要加入哪些特徵變數,比如說如果你在 Portland 蒐集各種房屋的資訊,你可以還會想要加入許多其他的資訊,像房屋裡面是否有壁爐、有幾間浴室等等,稍後會介紹更多變數的狀況。
而要進行監督式學習,必須先決定如何表示 \(h\) 這個函數,最簡單的方式就是選擇一個線性函數來逼近 \(y\):
\[h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2\]
這裡的 \(\theta_i\) 是所謂的參數(parameters),或稱為權重(weights),由這些參數來決定 \(h\) 函數如何把 \(\mathcal{X}\) 空間映射到 \(\mathcal{Y}\) 空間。在不會造成混淆的狀況下,你也可以把 \(h_\theta(x)\) 的 \(\theta\) 省略,直接寫成 \(h(x)\)。而為了簡化這條式子,我們設定截距(intercept)項為 \(x_0=1\),我們就可以把上面這條式子寫成:
\[h(x)=\sum^n_{i=0}\theta_ix_i=\theta^Tx\]
這條等式最右邊的 \(\theta\) 與 \(x\) 都是向量,而 \(n\) 則是輸入變數的數量(不包含 \(x_0\))。
現在我們建立好了 \(h\) 函數,而現在給我們一組 training set,那我們要如何來學習 \(\theta\) 呢?一個直覺的方式就是盡可能讓 \(h(x)\) 靠近 \(y\)(至少對於我們所拿到的 training examples),所以對於每一個 \(\theta\) 的值,我們定義了這樣的 cost function:
\[J(\theta)=\frac{1}{2}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\]
這個函數是針對每個 \(\theta\) 值,測量 \(h(x^{(i)})\) 有多靠近其所對應的 \(y^{(i)}\)。如果你學過回歸分析,你應該會發現這個跟最小平方法的回歸模型(least squares regression model)很像。
LMS 演算法
現在我們要找尋可以讓 \(J(\theta)\) 的值最小化的 \(\theta\),我們的做法是先「猜」一個初始值,然後依照 \(J(\theta)\) 的值不斷地更新 \(\theta\),直到最後找到可以讓 \(J(\theta)\) 最小的 \(\theta\),這裡我們使用 gradient descent 演算法,先指定一個 \(\theta\) 的初始值,然後根據這個遞迴式不斷的更新 \(\theta\):\[\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)\]
基本上每一個 \(\theta_j\) 都可以同時使用這個遞迴式子進行迭代,而 \(j=0,...,n\)。這裡的 \(\alpha\) 稱為 learning rate,在每個迭代中,\(\theta\) 會不斷的更新自己的值,而這個 \(\alpha\) 則控制每一步的大小。
這裡所使用的 \(:=\) 是表示在程式的撰寫時,使用等號右邊的值替換掉左邊變數內儲存的值(如果你會寫程式,應該瞭解這個概念)。
上面這個偏微分方程式可以進行一些簡單的推導,得到一個比較簡單的公式:
\[
\begin{aligned}
\frac{\partial}{\partial\theta_j}J(\theta) & = \frac{\partial}{\partial\theta_j}\frac{1}{2}(h_\theta(x)-y)^2\\
& = 2 \cdot \frac{1}{2}(h_\theta(x)-y) \cdot \frac{\partial}{\partial\theta_j}(h_\theta(x)-y)\\
& = (h_\theta(x)-y) \cdot \frac{\partial}{\partial\theta_j}\Big(\sum^n_{i=0}\theta_ix_i-y\Big)\\
& = (h_\theta(x)-y) x_j
\end{aligned}
\]
所以之前的遞迴式經過化簡之後,我們就可以得到每一個 training example 的遞迴公式:
\[\theta_j := \theta_j+\alpha\big(y^{(i)}-h_\theta(x^{(i)})\big)x_j^{(i)}\]
這個迭代方式稱為 LMS(least mean squares)演算法,也稱為 Widrow-Hoff 學習演算法,這個演算法的一些特性是比較自然且直覺的,像這個方法在更新 \(\theta\) 時,每次更新的距離會正比於它的 error 項 \(y^{(i)}-h_\theta(x^{(i)}))\),所以當我們的 \(\theta\) 已經很接近最佳解的時候(也就是 \(h_\theta(x^{(i)})\) 很接近 \(y^{(i)}\) 得時候),它的更新距離就會越來越短,到最後就不怎麼需要更新,而如果 \(\theta\) 距離最佳解還很遠,那麼它就會加緊腳步跑快一點。
以上我們已經推導出單一 training example 的狀況,接下來我們要把它拓展到 training set 的情況,方法有兩種,一種是這樣:
執行直到收斂 {
for every \(j\) {
\(\theta_j := \theta_j + \alpha\sum^m_{i=1}\Big(y^{(i)}-h_\theta(x^{(i)})\Big)x_j^{(i)}\)
}
}
你可以看得出來在這裡加總的那一項就是前面提到的 \(\partial J(\theta)/\partial\theta_j\),所以這其實就只是將 gradient descent 應用在 \(J\) 上而已,因為這樣的方式在每一次迭代時,需要將所有的資料都放進去算,所以稱為 batch gradient descent 方法。for every \(j\) {
\(\theta_j := \theta_j + \alpha\sum^m_{i=1}\Big(y^{(i)}-h_\theta(x^{(i)})\Big)x_j^{(i)}\)
}
}
這裡要注意一點,gradient descent 方法很容易受到 local minima 的干擾,所以找出來的解有可能不是 global minima,而因為這個例子我們的 \(J\) 是一個 convex quadratic function,所以只會有一個 global minima,沒有 local minima,所以使用 gradient descent 永遠都會收斂到 global minima。下面這張圖是應用在 convex quadratic function 的狀況:
圖中的橢圓就是這個二次函數的等高線(contours),那條路徑就是 gradient descent 的搜尋路徑,打叉叉的地方就是 \(\theta\) 每次迭代出來的值,他的起點在 (48, 30),最後收斂到中間的最小值。
我們使用 batch gradient descent 這個演算法計算前一個問題直到收斂之後,我們得到的 \(\theta_0=71.27\)、\(\theta_1=0.1345\),若將 \(h_\theta(x)\) 與 training set 的資料畫在一起,就會得到這樣的圖:
如果加上臥室的資料,則得到的結果為 \(\theta_0=89.60\)、\(\theta_1=0.1392\)、\(\theta_2=-8.738\)。
因為 batch gradient descent 在計算時,每一次的迭代都會需要所有 training set 的資料,但是如果 training set 的資料量太大的話,這樣迭代起來就會很花時間,這時候就可以使用另外一種演算法:
執行直到收斂 {
for \(i\) = 1 to \(m\) {
for every \(j\) {
\(\theta_j := \theta_j + \alpha\big(y^{(i)}-h_\theta(x^{(i)})\big)x_j^{(i)}\)
}
}
}
這個演算法在迭代的過程中,一次只使用單一個 training example 來計算 error 並更新 \(\theta\) 參數,這樣的演算法稱為 stochastic gradient descent 演算法,也叫做 incremental gradient descent 演算法,相較於 batch gradient descent 一次使用全部 training set 的方式,在樣本數 \(m\) 很大時,stochastic gradient descent 會比較容易進行計算,而且通常 stochastic gradient descent 演算法可以比較快速的靠近最佳解,也就是最小值的地方,但是它永遠不會收斂到最佳解,它只會在 \(J(\theta)\) 附近震盪而已,但實務上這個微小的誤差其實是可以接受的,因為它已經足夠接近最佳解了,也因為如此,在 training set 的資料很多的時候,stochastic gradient descent 會是比較好的選擇。for \(i\) = 1 to \(m\) {
for every \(j\) {
\(\theta_j := \theta_j + \alpha\big(y^{(i)}-h_\theta(x^{(i)})\big)x_j^{(i)}\)
}
}
}
繼續閱讀:史丹佛大學機器學習(Machine Learning)上課筆記(二)





沒有留言:
張貼留言